Set Type

The set type is a user-defined structured type.

It allows to implement the notion of set. This notion is fundamental in mathematics.

A set intuitively denotes a collection of distinct objects (the elements of the set).

The membership relationship connects an element and a set.

E = { a, b, c }
E is a set.
a ∈ E (a belongs to E.)

Set operations

Intersection of Sets

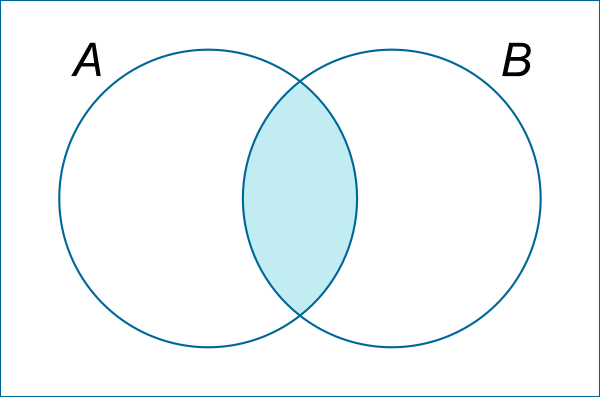
The intersection of two sets A and B is the set of elements which are in both sets A and B.
The intersection of the two sets is written as A ∩ B.

Union of Sets

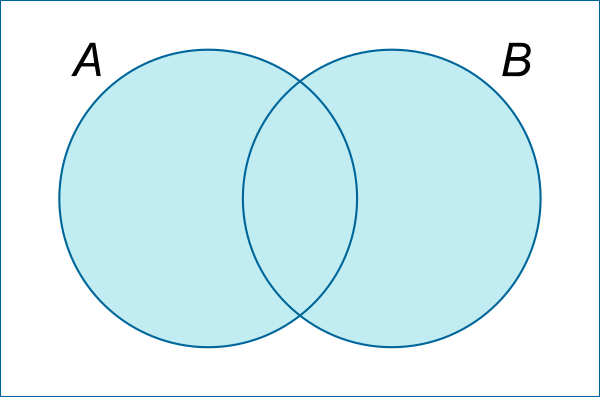
The union of two sets A and B is the set of elements which are either in A or B or in both sets A and B.
The union of the two sets is written as A ∪ B.

Difference of Sets

The difference of two sets A and B is the set of elements that contains exactly all elements in A but not in B.
The difference of the two sets is written as A \ B.

type
   identifier = set of ordinal_type;

Declaration

A variable of type set contains a set of elements of the same ordinal type.

Syntax: declaring a set type.

type
   identifier = set of ordinal_type;

Example: declaring a set type.

type
   letter = 'A'..'Z';
   alphabet = set of letter;
var
   vowels : alphabet;
   { . . . }
   vowels := ['A', 'E', 'I', 'O', 'U', 'Y'];

Operator in

The in operator corresponds to the membership relation in mathematics (a ∈ E). It produces a boolean value.

Syntax

element in some_set

Example

program example;
type
   letter = 'A'..'Z';
   alphabet = set of letter;
var
   vowels : alphabet;
   c : letter;
begin
   vowels := ['A', 'E', 'I', 'O', 'U', 'Y'];
   c := 'A';
   if c in vowels then
      writeln(c, ' is a vowel');
end.

Set operators

A set operator operates on two variables of the same set type.
It produce a result of the same set type as its operands.

Comparison operators

Two sets of the same type set can be compared by examining each element of both sets.

A comparison operator produces a boolean value.