Iterative Structure
An iteration refers to the execution of a sequence of instructions.
An iterative structure allows you to perform a series of iterations on the same sequence of instructions.
The terms loop and repetition are also used to designate an iterative structure.
Exit condition
A loop performs a certain number of iterations and then terminates.
To prevent a loop from iterating indefinitely, it is necessary to provide an exit condition which, when true, terminates the loop.
Counter
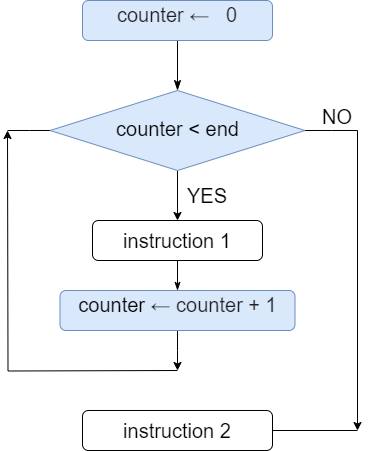
Sometimes a counter is used inside the loop to count the number of iterations already performed.
A counter is an integer variable, usually initialized to 0 and incremented with each new iteration.
The counter value is used in the exit condition to terminate the loop after a certain number of iterations.
for loop
The for loop allows you to perform a known number of iterations.
Syntax
for k := E1 to E2 do
I;
k is the loop counter, E1 and E2 are ordinal expressions of the same type as k.
E1 and E2 are the lower and upper limits of the range of successive values assigned to the counter k.
I is a loop statement that can be a sequence of statements.
When the loop instruction I is a sequence of instructions, we must delimit this sequence by the keywords begin and end.
The for loop implicitly manages the iteration counter and the exit condition.
The counter k is initialized to the value of E1.
The counter is incremented at each iteration, and the increment step, or increment, is 1.
When the counter value exceeds its upper limit E2, the exit condition is verified and the loop is terminated.
Loop instruction I is not executed if E1 > E2.
The value of the counter k cannot be modified in the body of the loop.
Syntax for a descending loop
for k := E2 downto E1 do
I;
Example: calculate the sum of the whole numbers from 1 to 9.
program example;
var
s, k : integer;
begin
s := 0;
for k := 1 to 9 do
s := s + k;
writeln(s);
end.
Nested loops
Example: multiplication table
program example;
var
i, j : integer;
begin
for i := 1 to 10 do
begin
for j := 1 to 10 do
write(i * j : 3);
writeln;
end;
end.
repeat loop
The repeat loop allows you to iterate until a condition is met.
Syntax
repeat I; until C;
I is a loop statement. C is a Boolean expression.
At the loop entry, I is executed, then C is evaluated.
If the value of C is true, then the exit condition is verified and the loop ends, otherwise we iterate from the loop entry.
At least one iteration is performed. The number of iterations is not known a priori.
In order to avoid an infinite loop, the value of C must be changed in the body of the loop so that its value is true at some point.
When the loop statement I is a sequence of statements, we do not need to delimit this sequence by begin and end, because the keywords repeat and until already play this role.
Example: implement a for loop using a repeat loop.
for loop
for k := E1 to E2 do
I;
repeat loop
k := E1; { initialize k }
m := E2; { evaluate E2 once and for all }
if k <= m then
repeat
I;
k := k + 1;
until k > m;
Example: calculate the sum of the whole numbers from 1 to 9.
program example;
var
s, k : integer;
begin
s := 0;
k := 1;
if k <= 9 then
repeat
s := s + k;
k := k + 1;
until k > 9;
writeln(s);
end.
while loop
The While loop allows you to iterate while a condition is true.
Syntax
while C do I;
I is a loop statement. C is a Boolean expression.
When the loop instruction I is a sequence of instructions, we must delimit this sequence by the keywords begin and end.
At the loop entry, C is evaluated.
If the value of C is true, then I is executed, and iteration is repeated from the loop entry.
The variables in the C expression must be initialized before the while loop entry, so that on the first pass, C can be evaluated.
In order to avoid an infinite loop, the value of C must be changed in the body of the loop so that its value is false at some point.
Example: implement a for loop using a while loop.
for loop
for k := E1 to E2 do
I;
while loop
k := E1; { initialize k }
m := E2; { evaluate E2 once and for all }
while k <= m do
begin
I;
k := k + 1;
end;
Example: calculate the sum of the whole numbers from 1 to 9.
program example;
var
s, k : integer;
begin
s := 0;
k := 1;
while k <= 9 do
begin
s := s + k;
k := k + 1;
end;
writeln(s);
end.
Loop selection
If the number of iterations is known a priori, then we use the for loop.
Otherwise we use the repeat loop when there is at least one iteration, or the while loop when the number of iterations can be zero.
Example: factorial
Write a program that calculates the value of the factorial of a natural number.
The factorial of a natural number n is denoted by n! and is defined as follows:n! = 1 x 2 x … x n
and by convention: 0! = 1.
program factorial;
var
n, f, k : integer;
begin
n := 6;
f := 1;
for k := 1 to n do
f := f * k;
writeln('factorial of ', n, ' is : ', f);
end.
Example: exponent
Write a program that calculates the value of the exponent of a natural number.
Program exponent;
var
m, n, p, k : integer;
begin
m := 2;
n := 3;
p := 1;
for k := 1 to n do
p := p * m;
writeln(m, ' raised to the power of ', n, ' is : ', p);
end.
Example: the Fibonacci sequence
Write a program that calculates the value of a term of the Fibonacci sequence.
Fibonacci sequence is defined as follows:
![]()
program fibonacci;
var
n, fibo, pred0, pred1, k : integer;
begin
n := 12;
if (n = 0) or (n = 1) then fibo := 1
else
begin
pred0 := 1;
pred1 := 1;
for k := 2 to n do
begin
fibo := pred0 + pred1;
pred0 := pred1;
pred1 := fibo;
end;
end;
writeln('the ', n, '-th Fibonacci number is: ', fibo);
end.
Example: prime number
Write a program that checks if a natural number is prime.
program prime;
var
n, k : integer;
p : boolean;
begin
n := 11;
if n = 1 then
writeln('not prime')
else
begin
k := 2;
p := true; {assume n is prime}
while (p = true) and (k < n) do
begin
if (n mod k) = 0 then
p := false;
k := k + 1;
end;
if p then
writeln(n, ' is prime')
else
writeln(n, 'is not prime');
end;
end.
Example: the greatest common divisor
Write a program that calculates the value of the greatest common divisor of two natural numbers.
Euclid’s algorithm allows us to find the GCD (greatest common divisor) of two natural integers m and n.
This algorithm works as follows:
- find the remainder of the division of m by n,
- then find the remainder of the division of n by the first remainder found,
- and so on until a zero remainder is found.
- The last divisor used is the GDC of m and n.
Example
Find the GDC de m = 1386 et n = 140.
Dividende
1386
140
126
Divisor
140
126
14
Euclidian division
1386 = 140 x 9 + 126
140 = 126 x 1 + 14
126 = 14 x 9 + 0
Remainder
126
14
0
The last divisor is 14, and therefore, the GCD of 1386 and 140 is 14.
program greatest_common_divisor;
var
m, n, a, b, r, gcd : integer;
begin
m := 1386;
n := 140;
a := m;
b := n;
r := a mod b;
while not(r = 0) do
begin
a := b;
b := r;
r := a mod b;
end;
gcd := b;
writeln('GCD of ', m, ' and ', n, ' is : ', gcd);
end.